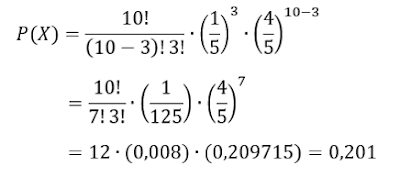Distribusi Binomial
Distribusi Binomial ditemukan oleh Jacob Bernaulli, ahli
Matematika berkebangsaan Swiss.
Distribusi binomial dikenal
juga sebagai distribusi Bernaulli.
Dalam teori
probablilitas, distribusi binomial merupakan
salah satu jenis distribusi probabilitas diskrit dengan jumlah
keberhasilan dalam n percobaan yang saling bebas, dimana setiap hasil percobaan
memiliki probabilitas p. Eksperimen berhasil/gagal juga disebut percobaan
bernoulli. Ketika n = 1, distribusi binomial adalah percobaan bernoulli.
Distribusi binomial merupakan dasar dari uji binomial dalam uji signifikansi
statistik.
Distribusi ini
seringkali digunakan untuk memodelkan jumlah keberhasilan pada
jumlah sampel n dari jumlah
populasi N. Sering dalam berbagai macam permasalahan
peluang hanya memiliki dua kemungkinan hasil atau dapat disederhanakan menjadi
dua kemungkinan.
Sebagai contoh,
ketika suatu koin dilempar, maka kita akan mendapat angka atau gambar. Ketika
seorang bayi lahir, maka seorang bayi tersebut merupakan bayi laki-laki atau
perempuan. Dalam permainan bola basket, tim yang bermain bisa menang atau
kalah. Keadaan benar/salah tersebut dapat
dijawab dengan dua
cara, yaitu benar
atau salah. Jika
peluang benar disimbolkan p, maka peluang gagal adalah q = 1-p.
Percobaan
binomial merupakan suatu percobaan yang memenuhi empat syarat berikut:
- Terdapat n kali
percobaan.
- Masing-masing
percobaan hanya dapat menghasilkan dua kemungkinan, atau hasil yang diperoleh
dapat disederhanakan menjadi dua kemungkinan.
Hasil yang diperoleh
tersebut dapat dianggap sebagai hasil yang sukses atau gagal.
- Hasil dari
masing-masing percobaan haruslah saling bebas.
- Peluang untuk
sukses harus sama untuk setiap percobaan.
Suatu percobaan binomial dan hasilnya memberikan distribusi peluang
khusus yang disebut sebagai distribusi binomial.
Hasil-hasil
percobaan binomial dan peluang yang bersesuaian dari hasil tersebut dinamakan
distribusi binomial.
Notasi-notasi yang umumnya digunakan dalam percobaan binomial distribusi binomial adalah
sebagai berikut.
P(S) : simbol untuk peluang sukses
P(F) : simbol untuk peluang gagal
p :
peluang sukses
q : peluang gagal
P(S) = p P(F) = q = 1 - p
n : banyaknya percobaan
X : banyaknya sukses dalam n kali
percobaan 0 <= X <= n dan X = 0,1,2,..., n
Rumus Peluang
Binomial
Dalam suatu
percobaan binomial, peluang untuk mendapatkan tepat X sukses dalam n percobaan
adalah :
Contoh 1
Suatu survey
menemukan bahwa satu dari lima orang berkata bahwa dia telah mengunjungi dokter
dalam sembarang bulan yang ditanyakan Jika 10 orang dipilih secara acak, berapa
peluang tiga diantaranya sudah mengunjungi dokter bulan lalu?
Pembahasan :
Pada kasus ini
Sehingga
Suatu koin
dilempar sebanyak tiga kali. Tentukan peluang mendapatkan tepat dua angka!
Pembahasan:
Ruang sampel dari
pelemparan satu koin sebanyak tiga kali adalah
S = { AAA, AAG, AGA, GAA, AGG, GAG, GGA, GGG } n(S) = 8
Dari ruang
sampel, kita dapat melihat bahwa ada tiga cara untuk mendapatkan tepat dua
angka, yaitu AAG, AGA, dan GAA. Sehingga peluang kita mendapatkan tepat dua
angka adalah 3/8 atau 0,375.
Contoh 2
Dengan melihat
kembali contoh ini dari sudut pandang percobaan binomial, maka memenuhi keempat
kriteria percobaan binomial.
- Terdapat tiga
kali percobaan.
- Setiap percobaan
hanya memiliki dua kemungkinan, yaitu angka (A) atau gambar (G).
- Hasil dari
masing-masing percobaan saling bebas (hasil dari suatu pelemparan tidak
mempengaruhi hasil pelemparan lainnya).
- Peluang percobaan
sukses (angka) adalah ½ di setiap percobaannya.
Oleh karena itu,
dapat kita lakukan perhitungan secara binomial
Jawaban tersebut
sama dengan jawaban sebelumnya saat kita menggunakan
rumus ruang sampel.
Sepasang suami
isteri yang baru menikah merencanakan untuk memperoleh empat
orang anak. Jika
rencananya mungkin terlaksana dan
diketahui probabilitas untuk memperoleh anak laki-laki dalam tiap kelahiran
adalah 0.51, maka:
- Probabilitas untuk memperoleh empat orang anak laki-laki:
- Probabilitas untuk memperoleh tiga orang anak laki-laki:
Probabilitas untuk memperoleh dua orang anak laki-laki:
Probabilitas untuk memperoleh satu orang anak laki-laki:
Probabilitas untuk memperoleh paling sedikit dua orang anak
laki-laki:
Oleh Nur Rohmah Oktaviani Putri, S.Si., M.Si
